Катеты прямоугольного треугольника

Влияние угла наклона на объем помещения мансарды

Если дом возводится с мансардой, то угол наклона скатов приобретает прикладное значение. И здесь соотношение прямое, то есть чем больше угол, тем больше объем мансарды. Чтобы было понятно, на фото ниже это хорошо видно.

Соотношение угла наклона скатов к объему мансардного помещенияИсточник legkovmeste.ru

Приведем пример, основанный на верхнем рисунке. Здесь четко видно, что высота помещения зависит от параметров наклона крыши. При этом надо учитывать, что оптимальная высота не должна быть меньше 2,5 м. А значит, угол наклона скатов мансарды минимально должна быть 25°

Но обратите внимание, что при таком расположении элементов кровли не учтен объем помещения. То есть ширина комнаты не будет больше 3 м

Это притом, что ширина дома – 10 м. Получается, что используется всего лишь 30% от пространства.

А значит, надо увеличивать значение угла. И чем больше он, тем больше полезная площадь мансарды. Но здесь есть обратная сторона медали. Увеличивая угол, увеличивается высота конька. А это расходы стройматериалов на возведение крыши, плюс увеличение парусности конструкции

Поэтому очень важно найти золотую середину. К примеру, 40° практически решают все проблемы

Чтобы отойти от этих проблем раз и навсегда, строители давно применяют совершенно другую конструкцию. Она сложна и в сооружении, и в проведении расчетов, но этот вариант решает проблему полезной площади помещения, не увеличивая высоту крыши.

Конструкция мансардной крышиИсточник ok.ru

Расчет высоты конька и угла наклона крыши:

Заключение по теме

Проведение расчетов кровельной конструкции – прерогатива специалистов. Потому что правильный расчет, того же угла наклона, это надежность крыши в целом. Но ориентироваться в некоторых технических понятиях будет полезно и владельцам строящихся домов.

Разуклонка кровли

Разуклонка – это ряд мероприятий, применяемых для создания наклона на плоских крышах, устройства на них коньков и ендов. Благодаря этому уклон односкатной крыши способствует решению проблем с накоплением осадков на ее поверхности. Уклон нужно просчитать заранее. ещё до того, как сделать односкатную крышу. Минимально допустимым показателем для плоских кровель считается величина 1,5 градуса (подробнее: «Какой минимальный уклон плоской кровли «). Наклон ската необходимо обустроить таким образом, чтобы вода с его поверхности стекала в водоприемные воронки. Для этих целей применяют керамзит или цементные стяжки, но последние значительно увеличивают нагрузку на кровлю.

Если разуклонку выполняют при проведении ремонта, а не при строительстве нового здания, тогда используют плитные материалы, а также пенополиуретан или пенобетон.

Какую кровлю выбрать, подробнее на видео:

Проценты на дорожном знаке — важное предупреждение?

Тихое раннее утро. Самое время делать добро. Что может быть лучше подарка нашим матерям — какого-нибудь скромного букетика. Но букета не цветов, а некоторых необходимых в жизни женщины-автолюбителя знаний!

Вы уже обращали внимание на предупреждающие дорожные знаки с черным треугольником, символизирующим спуск или подъем, и количеством процентов, обозначающим крутизну этого спуска (или подъема)? И, возможно, задавали себе вопрос — а, например, 12% — это сколько? И почему бы крутизну уклона не обозначать в градусах?

На этих знаках обозначен тангенс угла наклона, выраженный в процентах.

Ну вот, ваша улыбка увяла, словно, развернув пакет с подарком, вы обнаружили в нем увесистый том Достоевского. А ведь уже через несколько минут вы будете непринужденно оперировать понятием «тангенс», а заодно «синус» и «косинус», удивляясь тому, что до сегодняшнего дня они заставляли вас напрягаться.

Итак, прислоните лыжную палку углом к стене напротив яркой лампы. Вы увидите две тени — одну на стене, другую на полу. Учителя, чтобы вас позлить, называли эти тени проекциями. Соответственно, на вертикальную и горизонтальную плоскости. Та тень, что на стене, называется «синус», та, что на полу — «косинус».

Чем ближе к стене вы придвинете низ палки, тем короче будет «косинус». Наоборот, отодвигая низ палки от стены, вы увидите, что «синус» становится все меньше, а «косинус» — больше. Отношение синуса к косинусу называется тангенсом.

Если вы установите палку под углом 45 градусов от пола, синус и косинус будут совершенно одинаковы. В таком случае тангенс будет равен 1. Или, как говорили ваши учителя, тангенс 45 градусов равен 1.

Если мы посмотрим сбоку на дорогу, в том месте, где она имеет уклон, то увидим, что угол этого уклона находится в пределах 8 градусов от горизонта. Высота подъема, или «синус», гораздо меньше, чем длина проекции дороги на горизонтальную плоскость — «косинус». Разделив высоту подъема на длину горизонтальной проекции, обнаружим, что тангенс угла такого уклона не превышает 0,12.

Его удобно выражать в процентах — например, 12%. В таком случае тангенс угла 45 градусов равен 100%.

Теперь вы уже смело можете использовать эту информацию. Так, проехав 1 километр по дороге с уклоном 12%, вы подниметесь (или спуститесь) на 120 метров. (При таких небольших углах уклона длину горизонтальной проекции дороги можно считать равной длине дороги).

Из любопытства вы можете перевести угол уклона обратно в градусы с помощью калькулятора на сотовом телефоне, настроив его на «научный» режим, например: TAN -1 (0,12)=7 градусов. В некоторых калькуляторах: ATAN (0,12)=7.

Впрочем, для автолюбителей главное не это. Надеюсь, вы уже прочли мою статью о коэффициенте сцепления.

Так вот, оказывается, тангенс угла наклона равен коэффициенту сцепления.

Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (Это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой.)

Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. Так, при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину.

И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки с черным треугольником и цифрами внутри. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае — не сможете сдвинуться с места. А уж если затормозите на спуске…

Но я убежден, что теперь ничего такого с вами не случится. И от души надеюсь, что сегодня хоть чуточку помог вам, дорогие матери — наша самая ответственная и любимая часть человечества.

Уклон в процентах

Уклоны в градусах и процентах 1º — 1,7 % 1 % — 34′ 20″ Просто для справки.

вы бы не позорились, утверждать что величина уклона прямо и линейно пропорциональна углу — это просто незнание основ математики! или просто дезинформация! «по секрету»: уклон — это отношение противолежащего катета к прилежащему — в математике называют «тангенс угла», теперь откройте учебник и посмотрите график этой функции — как видите, он совсем не похож на прямую линию.

Даже простейший пример: угол 45º. а уклон = 100% — это уже в вашу формулу не вписывается. или вы считаете что при 45º катеты не равны ?

в некоторых документах увидел что этот уклон пишут намного больше, с чем это связано?

так может с тем и связано — что уклон в некоторых случаях намного больше! у нас например некоторые и уклон скатной кровли до сих пор пишут в долях, а не в градусах. так что если сравнивать уклон в долях для дороги и уклон для ската кровли — разница может быть огромной, но в этом нет ошибки.

Как узнать угол наклона крыши

Между уклоном кровельных скатов и снежной нагрузкой имеется прямая зависимость. Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.

Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.

Высота крыши в коньке определяется следующим образом:

• Первым делом нужно рассчитать ширину пролета;
• Полученная величина делится на 2;
• Чтобы сделать расчет высоты конька, результат предыдущего расчета умножается на коэффициент, соответствующий определенному углу наклона.

На примере реализация такой методики расчета выглядит так: при ширине здания, равной 8 метрам, и 25-градусном уклоне кровли, расчетный коэффициент составляет 0,47. В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.

Как измерить уклон

Таблица соотношения градус/процент уклона кровли.

На графике ищем наклонную линию, с которой стыкуется дугообразная стрела 2. Пересечение наклонной линии c вертикальной шкалой определяет уклон, минимально допустимый для данной крыши, который равен 50%. Нам известно, что уклон ската определяется отношением высоты конька к половине его заложения. Произведем расчет таким образом:

i = 10 метров (заложение)

h = 4 метра (высота конька)

i= h / (1/2) = 4 / (10/2) = 0,8

Для того чтобы измерить уклон в %, это отношение умножают на 100

Таким образом, уклон в 80% при соблюдении норм строительства обеспечит достаточный сброс дождевой воды со всей площади. Для кровли из рулонных полимерно-битумных, битумных и мастичных материалов с уклоном 10° необходим защитный слой для основного водоизоляционного покрова из гравия либо каменной крошки, у которой марка морозостойкости не меньше 100. Такой же защитный слой применяется для кровли крыши с помощью пленочных рулонных материалов с углом до 2,5%. Слой для защиты из гравия должен быть толщиной 1-1,6 см, а слой крупнозернистой посыпки — 0,3-0,5 см.

Причем на крышах с уклоном примерно до 2,5% с использованием эластомерных пленочных материалов в рулонах, выполненных свободной кладкой, необходим утяжеляющий слой гравия из расчета 50 кгс/кв.м.

На крышах из битумно-полимерных или битумных покрытий в рулонах с углом наклона выше 10% верхний слой гидроизоляционного покрова выполняется из крупнозернистой посыпки. На крышах из мастичных материалов с углом больше 10% предусматривается защитный слой из красочных составов.

При создании крыши из асбестоцементных листов, а также профнастила и металлической черепицы с наклоном до 20% по всей площади необходимо производить герметизацию стыков. Не более чем на 5% можно допустить отклонение уклона кровли из мелкоштучных материалов. Производя эти расчеты, можно узнать площадь помещения мансарды или чердака.

Расчет угла, если заданы три точки в прямоугольной системе координат

В этом случае проще будет разобраться с объяснениями сразу на примере.

Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между \(\overrightarrow{AC}\) и \(\overrightarrow{BC}\).

Решение

Для начала найдем их координаты по известным координатам заданных точек:

\(\overrightarrow{AC}=(6-3, -1-(-2))=(3,1)\)

\(\overrightarrow{BC}=(6-2, -1-1)=(4,-2)\)

После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:

\(\cos\left(\widehat{\overrightarrow{AC};\overrightarrow{BC}}\right)=\frac{(\overrightarrow{AC};\;\overrightarrow{BC})}{\left|\overrightarrow{AC}\right|\cdot\left|\overrightarrow{BC}\right|}=\frac{3\cdot4+1\cdot(-2)}{\sqrt{3^2+1^2}\cdot\sqrt{4^2+{(-2)}^2}}=\frac{10}{\sqrt{10}\cdot2\sqrt5}=\frac{10}{10\sqrt2}=\frac1{\sqrt2}\)

Ответ: \(\cos\left(\widehat{\overrightarrow{AC};\overrightarrow{BC}}\right)=\frac1{\sqrt2}.\)

Единицы измерения угла ската кровли

Какой угол наклона односкатной крыши (двускатной, шатровой и так далее) принят, может указываться в:

• градусах;
• процентах;
• дробном числе.

При этом под градусами понимается угол к горизонтали, проценты или дробь – отношение высоты конька к половине ширины крыши (в строительстве используется термин «заложение»).

Измерение угла наклона крыши

Измерение в градусах относительно неточное, дает (в зависимости от используемого инструмента) погрешность до 5% по углу и до 10% по линейным размерам строения при расчетах. Более точные результаты дает измерение в процентах, причем за 100% принят угол в 45 градусов.

Для более удобного использования обеих измерительных систем приведена таблица, позволяющая переводить угол наклона крыши (градусы) в проценты и наоборот.

Для расчета используется стандартная схема:

При таких параметрах процентное выражение угла кровли составляет 5:8 х 100% = 62,5%, в градусах это значение составит примерно 32о, в дробном выражении – 5:8 = 1:1,6.

Для лучшего понимания того, как и какими инструментами производится замер наклона крыши, как рассчитать скат крыши, предлагаем посмотреть видео.

Как рассчитать угол наклона двускатной крыши

Расчет наименьшего и оптимального уклона крыши предполагает определение потенциальной нагрузки на кровлю в процессе эксплуатации с учетом 2-х показателей:

• массы сооружаемой конструкции;
• нагрузка снежных масс, оказываемая на конструкцию (для конкретного региона).

Расчет массы сооружаемой конструкции. Так, для 2-х скатной стандартной крыши определяют массу 1 кв.м. каждого слоя конструкции, полученные данные суммируются. Общее значение перемножается на коэффициент запаса, имеющий значение 1,1. Введение этого коэффициента позволяет, в случае необходимости, выполнить смену кровельных материалов и утяжелить конструкцию. Среднестатистическая нагрузка на 1 кв.м. кровли жилых строений не превышает более полусотни кг

Важно помнить, что для многих кровельных покрытий применяется существенно завышенный показатель.

Выбор коэффициента снежной нагрузки в зависимости от угла уклона:
не более 25 градусов – 1,0;
25-60 градусов – 1,25.

При наклоне более 60 градусов снеговая нагрузка не учитывается.

Определение угла наклона крыши:

• значение ширины пролета разделить пополам (а);
• выполнить расчеты по формуле.

Sin A=a/ b. где А – угол наклона, а – половина ширины фронтона, b – высота фронтона.

В вычислении угла наклона обращаются к таблицам Брадиса.

Расчет длины стропил выполняется по формуле:

Lc=Hk/sinA. где Lc – длина стропил, Hk – высота конька, А – угол наклона

Пример расчетов

Рассмотрим примеры расчета угла наклона:

1. Двухскатная крыша, на чердаке которой планируется обустроить помещение мансардного типа.
   • В этом случае высота конька стандартная и равна 1,8 м.
   • Ширина фронтона также известна и составляет 6 м. а=6/2=3, Sin A=a/b=3/1,8=1,67
   • В таблице Брадиса находим значение угла наклона при Sin A=1,67. Приблизительное значение 58-59 градусов. Можно округлить до 60.
2. Односкатная крыша Строение имеет длину стены 5 м, угол наклона выбран в 25 градусов.

• Определение высоты стены: Нстены=5×tg25°=5×0,47=2,35 метра
• Определение длины стропил: Lстропил=2,35÷sin25°=2,35÷0,42=5,6 метра
• К полученному значению добавляют длину заднего и переднего свеса стропил, позволяющих защитить строение от осадков.

Конечно же, сооружение крыши лучше поручить специалистам. Однако, при самостоятельном выполнении правильного расчета кровли, после завершения строительства будет получен не только эстетичный, но и функциональный готовый продукт.

• Расчет показателей для возведения мансардной…
• Проекты домов с односкатной крышей: варианты…
• Монтаж стропильной системы двухскатной крыши
• Стропильная система полувальмовой крыши
• Укладка мягкой кровли своими руками:…
• Как сделать односкатную крышу своими руками

В чем измеряется угол уклона крыши

  Обозначение уклона кровли на чертежах может быть как в градусах, так и в процентах. Уклон крыши обозначается латинской буквой i.

  В СНиПе II-26-76, данная величина указывается в процентах ( % ). В данный момент не существует строгих правил по обозначению размера уклона крыши.

  Единицей измерения уклона крыши считают градусы или проценты ( %). Их соотношение указаны ниже в таблице.

Уклон крыши соотношение градусы-проценты

градусы	%		градусы	%		градусы	%
1°	1,75%	16°	28,68%	31°	60,09%
2°	3,50%	17°	30,58%	32°	62,48%
3°	5,24%	18°	32,50%	33°	64,93%
4°	7,00%	19°	34,43%	34°	67,45%
5°	8,75%	20°	36,39%	35°	70,01%
6°	10,51%	21°	38,38%	36°	72,65%
7°	12,28%	22°	40,40%	37°	75,35%
8°	14,05%	23°	42,45%	38°	78,13%
9°	15,84%	24°	44,52%	39°	80,98%
10°	17,64%	25°	46,64%	40°	83,90%
11°	19,44%	26°	48,78%	41°	86,92%
12°	21,25%	27°	50,95%	42°	90,04%
13°	23,09%	28°	53,18%	43°	93,25%
14°	24,94%	29°	55,42%	44°	96,58%
15°	26,80%	30°	57,73%	45°	100%

  Перевести уклон из процентов в градусы и наоборот из градусов в проценты можно при помощи онлайн конвертера:

Замер уклона крыши

  Измеряют угол уклона при помощи уклономера или же математическим способом.

  Уклономер — это рейка с рамкой, между планками которой есть ось, шкала деления и к которой закреплён маятник. Когда рейка находится в горизонтальном положении, на шкале показывает ноль градусов. Чтобы произвести замер уклона ската крыши, рейку уклономера держат перпендикулярно коньку, то есть в вертикальном уровне. По шкале уклономера маятник указывает, какой уклон у данного ската крыши в градусах. Такой метод замера уклона стал уже менее актуален, так как сейчас появились разные геодезические приборы для замеров уклонов, а так же капельные и электронные уровни с уклономерами.

Математический расчёт уклона

  Можно рассчитать уклон крыши не используя геодезические и другие приборы для замеров уклона. Для этого необходимо знать два размера:

• Вертикальная высота ( H ) от верхней точки ската (как правило конька) до уровня нижней (карниза)
• Заложение ( L ) — горизонтальное расстояние от нижней точки ската до верхней

  При помощи математического расчёта величину уклона крыши находит следующим образом:

Угол уклона ската i равен отношению высоты кровли Н к заложению L

i = Н : L

  Для того, чтобы значение уклона выразить в процентах, это отношение умножают на 100. Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.

  Чтобы было понятней рассмотрим на примере:

Пусть будет:

Длина заложения 4,5 м, высота крыши 2,0 м.

Уклон равен: i = 2.0 : 4,5 = 0,44 теперь умножим на × 100 = 44 %. Переводим данное значение по таблице в градусы и получаем — 24°.

Минимальный уклон для кровельных материалов (покрытий)

Вид кровли	Минимальный уклон крыши
в градусах	в %	в соотношении высоты ската к заложению
Кровли из рулонных битумных материалов: 3-х и 4-х слойные (наплавляемая кровля)	0-3°	до 5%	до 1:20
Кровли из рулонных битумных материалов: 2-х слойные (наплавляемая кровля)	от	15
Фальцевая кровля	от 4°
Ондулин	5°		1:11
Волнистые асбоцементные листы (шифер)	9°	16	1:6
Керамическая черепица	11°		1:6
Битумная черепица	11°		1:5
Металлочерепица	14°
Цементно-песчанная черепица	34°	67%
Деревянная кровля	39°	80%	1:1.125

Минимальный уклон кровли

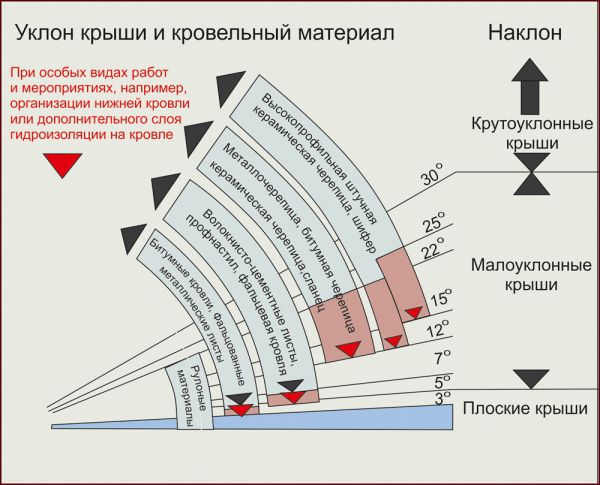
Кровельный материал, являющийся одним из главных элементов структуры верхней плоскости, также предусматривает определенные рекомендации уклона в зависимости от своего типа.

• В случае с профнастилом устанавливают угол на уровне 12 градусов, для металлочерепицы данный показатель следует увеличить до 15º.
• Ондулин или мягкую черепицу на простонародном языке можно укладывать при склоне в 11 градусов. Вот только в этом случае также есть один нюанс, который заключается в сплошной обрешетке.
• При укрытии керамической черепицы наклон должен быть минимум 22º. Также стоит учесть, что стропильная система поддается большим нагрузкам в случае небольшой наклонности ската. Во избежания перегрузок следует этот фактор взять на вооружение во время проектирования.
• К самым распространенным видам поверхностного покрытия относится шифер. При настилании асбестоцементных волнистых листов показатель склона кровли не должен превышать 28%. Те же требования и к стальным плоскостям.
• Минимальный уклон кровли из сэндвич панелей по нормам составляет 5 градусов, если планируются окна в панелях, то уклон увеличивается до 7 градусов.

По какому СНиП посмотреть уклон кровли? Оптимальный и минимальный уклон кровельного материала вы можете посмотреть в СНиП II-26-76 Кровли.

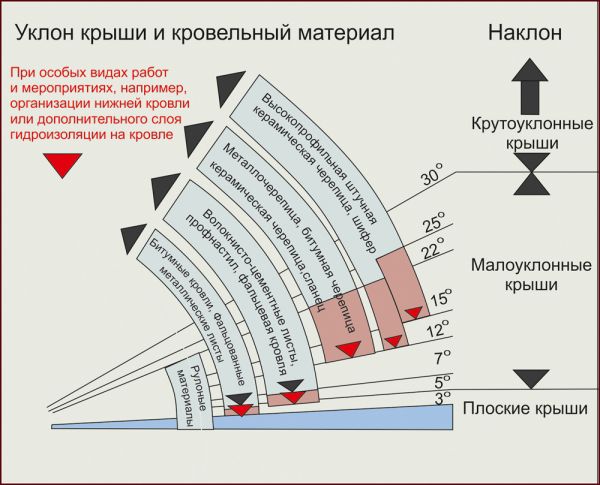
Зависимость уклона от выбора кровельного покрытия

Признаки равенства прямоугольных треугольников

1. Признак равенства прямоугольных треугольников по двум катетам

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то эти треугольники равны.

Действительно. Пусть , (Рис.3). Поскольку , то по первому признаку равенства треугольников следует, что треугольники и равны.

2. Признак равенства прямоугольных треугольников по катету и прилежащему к нему острому углу

Если катет и прилежащий к нему острый угол прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Действительно. Так как , , (Рис.4), то из второго признака равенства треугольников следует, что треугольники и равны.

Теорема 1. Если гипотенуза и прилежащий к нему острый угол прямоугольного треугольника соответственно равны гипотенузе и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Доказательство. Пусть и (Рис.5). Так как данные треугольники прямоугольные, то имеет место также равенство . Тогда из второго признака равенства треугольников следует, что треугольники и равны.

4. Признак равенства прямоугольных треугольников по гипотенузе и катету

Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Доказательство. Рассмотрим треугольники и , где , и углы C и C₁ прямые (Рис.6).

Поскольку , , , то треугольник можно наложить на треугольник так, чтобы вершина C совместилась с верншиной C₁ а стороны CA и CB наложились на лучи C₁A₁ и C₁B₁, соответственно (Рис.7).

Так как CB=C₁B₁, то вершина B совместится с вершиной B₁. Покажем, теперь, что вершина A совместится с вершиной A₁. Предположим, что они не совместятся. Тогда получим равнобедренный треугольник ABA₁, поскольку AB=A₁B₁. Но в этом случае . Но как мы видим из Рис.7 угол , острый а угол тупой (так как он является смежанным углом к острому углу BAC), что невозможно. Следовательно вершина A совместится с вершиной A₁.

Как узнать уклон дороги отчёт, 2017 год

Уклон 12%, сколько это в градусах? | Автор топика: Артем

Помогите, пожалуйста, разобраться: что такое уклон 12%? Сколько это будет в градусах и есть ли вообще разница в процентах от градусов? Заранее благодарю.

Евгений Означает перепад высот на 12 м по вертикали на 100 м пути..

Роман 12% от 90 градусов.

Илья 360 — 100%, дальше сам

Артём разница есть конечно: 12%=10,8 градусов

Иван примерно 7 град

Ярослав сколько процентов столько и градусов. а то понимешь градусы они и в температуре тоже градусы и в спиртном градусы, а то дорожный знак может в заблуждение ввести.)))

Денис уклон 12% — это отношение высоты к длине основания. Поэтому уклон 100% — это 45 градусов, а 12% — это примерно 6,85 градусов, он же тангенс

Петр проценты это возвышение, метров вертикальных на сто метров горизонтальных решите как прямиоугольный треугольник отношение сторон это тангенс угла. извлечь арктангенс получите угол

Константин Уклон дороги — относительное превышение одной точки продольного Григорий профиля дороги над другой, определяемое как отношение превышения к горизонтальному расстоянию между двумя точками. Уклон 10% Это отношение высоты подъёма в 10 метров к горизонтальной проекции дороги длинной 100метров. В геометрическом смысле — это тангенс угла подъёма дороги. Чтобы перевести уклон из процентов в градусы надо уклон дороги в процентах разделить на100 и полученную велину посмотреть в таблице Брадиса раздел Тангенсы.

Для уклона 10% угол уклона в процентах будет примерно tgВалерий -0.105 Шесть градусов. Для уклона 100% угол наклона 45 градусов.

Михаил Это надо понимать также, как говорят: скидка цен на товары 40%, спрашивается от двух милионов скидывают или от трёх, а другой спрашивает, с какого этажа скидывают с пятого или с девятого?

Леонид уклон измеряется в промилле и имеет отношение длинны от высоты. 1 промилле равен 1 метру в высоту на 1000 метров длины все ответы из википедии. я окончил автодор на фак. строительство дорог.

Степан Это 6град. 50′ 33.98″ или 6.84град. Но это неудобно. Считайте, так, как предлагает выше Виктор. Это удобно.

Помогите, пожалуйста, разобраться: что такое уклон 12%? Сколько это будет в градусах и есть ли вообще разница в процентах от градусов? Заранее благодарю.

Никита Крутизну подъемов и спусков дорог называют уклоном. Величину уклона выражают в процентах и определяют по формуле:

i = Артём * 100

где h — высота подъема или спуска; L — длина подъема или спуска.

Уклон, равный 1%, обозначает подъем или спуск на 1 м на каждые 100 м дороги. Наибольшие продольные уклоны на автомобильных дорогах Poccuu не превышают 6 — 7% на равнинной и холмистой местности и 9 — 10% в горах. Конвенция о дорожных знаках и сигналах Виктор Договаривающиеся стороны, признавая, что единообразие дорожных знаков, сигналов и обозначений и разметки дорог в международном плане необходимо для облегчения международного дорожного движения и повышения безопасности на дорогах.

Станислав Курсовик Лепиш?, Удачи, а то ко Мне в Часть Попадёшь!

Денис На железной дороге величина уклона измеряется не в процентах, а в промилле. Т. е. «одна тысячная» уклона — спуск на 1 метр на 1 км расстояния. На автодорогах — так же, только измеряется в процентах. Т. е. на 100 м. расстояния.

Детский город из бумаги

Jul 7, 2014 — Хотите создать огромный город из бумаги прямо у себя на столе? … Для придания городу подобающего вида можно сделать различные здания и … Для того, чтобы построить автомобильную или железную дорогу …

tomnosti.info

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже

Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б

Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Уклон кровли в процентах и градусах

Как определить угол наклона крыши в градусах? Наклонный угол, как и любая подобная фигура согласно геометрическим канонам, измеряется в градусах.

Но во многих документах, в том числе и СНиПах, данная величина отображается в процентах, поэтому нет строгих требований и обоснований, чтобы руководствоваться только одной единицей измерения.

Главное в этой ситуации — знать пропорции для соотношения, если вдруг понадобится перевести градусы в проценты и наоборот, к примеру, для удобства во время вычислительных действий.

В целом, коэффициент пересчета градусов на проценты колеблется с 1,7 (для 1 градуса) до 2 (для 45 градусов). В тех случаях, когда принципиально важны показатели, выраженные не целым процентом, в цифровом отображении применяют промилле — сотые доли %.

Если доверять теории, то наклонности могут достигать 60 и даже 70 градусов, но на практике это будет выглядеть не совсем целесообразно. Да и по внешнему виду впечатление «так себе», разве что Ваш дом расположен где-то в Альпах и нужно соорудить крышу, которая постоянно испытывает на себе снеговые нагрузки.

Перевод градусов в проценты

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Катет a = Катет b = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Катет (a или b) = Прилежащий угол (β или α) = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

c = a/_cos(β) = b/_cos(α)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Катет (a или b) = Противолежащий угол (α или β) = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

c = a/_sin(α) = b/_sin(β)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Гипотенуза c = Катет _{(известный)} = Катет _{(искомый)} =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

a = √c² — b²

b = √c² — a²

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √5² — 4² = √25 — 16 = √9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Гипотенуза c = Угол (прилежащий катету) = °Катет =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

a = c ⋅ cos(β)

b = c ⋅ cos(α)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Гипотенуза c = Угол (противолежащий катету) = °Катет =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

a = c ⋅ sin(α)

b = c ⋅ sin(β)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Катет (известный) = Угол (прилежащий известному катету) = °Катет (искомый) =

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

a = b ⋅ tg(α)

b = a ⋅ tg(β)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Катет (известный) = Угол (противолежащий известному катету) = °Катет (искомый) =

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

a = b / tg(β)

b = a / tg(α)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см